
 벡터의 내적 코사인 공식 증명
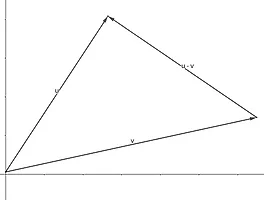
DirectX 12를 이용한 3D 게임 프로그래밍 입문 연습문제 제 1장 10번 문제다. 제 2의 코사인 법칙을 통해 내적 공식을 증명해보자. 삼각형 세 변의 길이를 $a, b, c$라고 했을 때, 제 2의 코사인 법칙을 적용하면 다음과 같다.여기서 삼각형 세 변의 길이를 각각 $a=||u||,\ \ b=||v||,\ \ c=||u-v||$라고 하면 다음과 같이 표현할 수 있다. 여기서 양변에 음수를 곱하고 $2||u||||v||cos{\theta}$를 제외하고 좌항으로 넘겨보자. 그런 다음 $u=\{u_x, u_y, u_z\},\ \ v=\{v_x, v_y, v_z\}$라고 정의하고 좌항을 모두 전개해보자.이미 크기의 제곱이므로 제곱근은 고려하지 않아도 된다. 따라서 다음과 같다.증명 끝~
벡터의 내적 코사인 공식 증명
DirectX 12를 이용한 3D 게임 프로그래밍 입문 연습문제 제 1장 10번 문제다. 제 2의 코사인 법칙을 통해 내적 공식을 증명해보자. 삼각형 세 변의 길이를 $a, b, c$라고 했을 때, 제 2의 코사인 법칙을 적용하면 다음과 같다.여기서 삼각형 세 변의 길이를 각각 $a=||u||,\ \ b=||v||,\ \ c=||u-v||$라고 하면 다음과 같이 표현할 수 있다. 여기서 양변에 음수를 곱하고 $2||u||||v||cos{\theta}$를 제외하고 좌항으로 넘겨보자. 그런 다음 $u=\{u_x, u_y, u_z\},\ \ v=\{v_x, v_y, v_z\}$라고 정의하고 좌항을 모두 전개해보자.이미 크기의 제곱이므로 제곱근은 고려하지 않아도 된다. 따라서 다음과 같다.증명 끝~

