참고 사이트
사전 지식
자료 구조인 트리에 대한 용어와 개념을 알고 있어야한다. 또한 이진 트리에서 사용하는 Left Rotate와 Right Rotate에 대해 알고 있어야한다. 트리와 이진 트리에 대해 먼저 학습한 뒤 레드-블랙 트리를공부하는 것을 추천한다.
어원
위키 백과에 따르면, 레드-블랙 트리의 이름은 다음과 같다.
레드-블랙 트리(red-black tree)는 자가 균형 이진 탐색 트리(self-balancing binary search tree)로서, 대표적으로는 연관 배열 등을 구현하는 데 쓰이는 자료구조다.
자가 균형 이진 탐색 트리라 하면은 어떤 존재인지 알겠는데, 왜 하필 레드-블랙 트리라는 이름으로도 불려지는 걸까? 레드-블랙 트리의 작동 원리를 보면 색깔을 구분하여 균형을 맞추는건 알겠지만, 왜 하필 빨간색과 검은색으로 구분짓게 된 걸까?
In a 1978 paper, "A Dichromatic Framework for Balanced Trees",[7] Leonidas J. Guibas and Robert Sedgewick derived the red–black tree from the symmetric binary B-tree.[8] The color "red" was chosen because it was the best-looking color produced by the color laser printer available to the authors while working at Xerox PARC.[9] Another response from Guibas states that it was because of the red and black pens available to them to draw the trees.[10]
단순하게 컬러 레이저 프린터에서 가장 잘 보이는 색깔이였다고 한다. 이 트리를 고안한 사람이 편하게 사용할 수 있었던 색깔이였기 때문인 것 같다.
목적
C++ STL 중 map과 set을 구현하기 위해서는 이 레드-블랙 트리를 이해하고 넘어가야 하기 때문에 이 노션을 작성하게 되었다. 강의에서 자료구조 수업을 들었지만, 이진 트리와 2-3 트리 등 여러 트리에 대한 설명과 실습을 진행해보았지만, 정작 중요한 레드-블랙 트리에 대해서는 난해한 설명과 실습하는 시간을 갖지 못해서 아쉬웠다. 따라서 독학으로 공부하여 C++ STL을 이해하는데 도움이 되었으면 하는 마음이다.
원리
우선 균형 이진탐색트리(Balanced Binary Search Tree) 중 하나의 트리로 삽입과 삭제가 일어날 때, 어떻게 균형 이진탐색트리로 만들 수 있는가에 대한 방법 중 하나가 바로 레드-블랙트리인 것이다.
또 하나에 방법으로는 AVL 트리가 있는데, 레드-블랙 트리와의 차이점은 참고 문헌으로 남긴다.
Red Black Tree vs AVL Tree - GeeksforGeeks
삽입
레드-블랙 트리는 각 노드마다 1bit인 색깔 정보를 가지고 이 정보를 토대로 균형있는 트리를 구성한다. 그리고 4개의 규칙이 있는데, 이 규칙들은 다음과 같다.
- 레드-블랙 트리의 조건
- Root Property : 루트노드의 색깔은 검정(Black)이다.
- External Property : 모든 external node들은 검정(Black)이다.
- Internal Property : 빨강(Red)노드의 자식은 검정(Black)이다.
- == No Double Red(빨간색 노드가 연속으로 나올 수 없다.)
- Depth Property : 모든 리프노드에서 Black Depth는 같다.
- == 리프노드에서 루트노드까지 가는 경로에서 만나는 블랙노드의 개수는 같다.

2번 조건에서 external node는, NIL 노드를 의미한다. 자식이 1개 이하인 노드들에게 NIL 노드를 붙여주는 것이다.
위에 4가지 조건들을 만족하면 비로소 균형 이진 트리를 만들 수 있는 것이다. 문제는 저 조건들을 만족하기 위해 삽입과 삭제 시 처리해야할 작업들이 있다.

삽입되는 값은 무조건 Red이고, 트리에 값을 넣다보면 저렇게 3번 규칙을 위배하는 상황이 발생한다.
그럼 3을 그냥 검정색을 바꾸면 되는거 아니냐? 할 수 있지만 균형을 맞추기 위해서는 좀 더 복잡한 방법이 필요하다. 그래서 Restructuring 과 Recoloring 방법을 사용하는데, 이 방법을 사용하는데에도 조건이 있다.
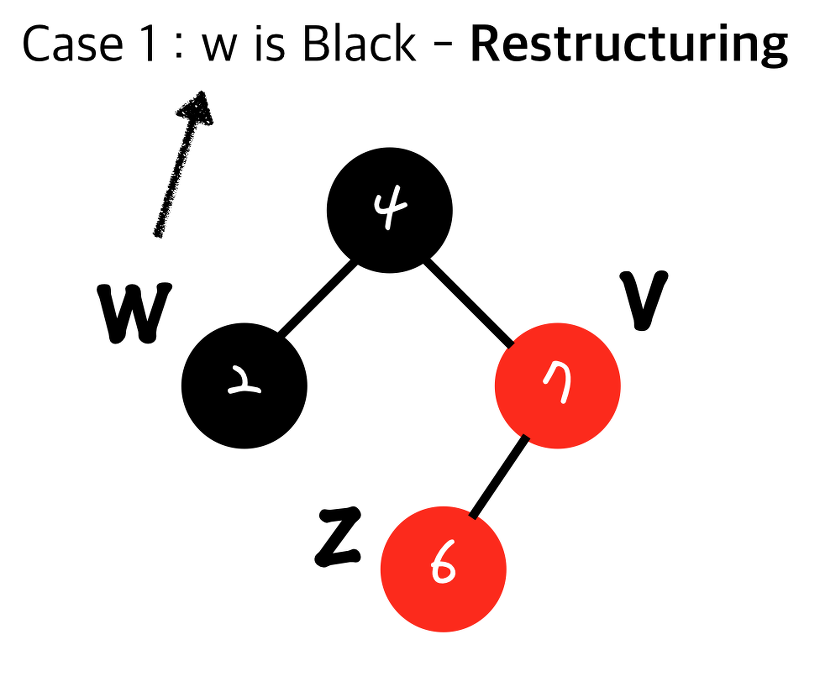

Parent Node를 $v$, 삽입된 노드를 $z$, $z$의 uncle node를 $w$라고 하자.
Double Red가 발생하면, 현재 삽입한 노드의 uncle node($w$)의 색깔에 따라 결정된다.
즉, $w$가 검정색이면 Restructuring, 빨간색이면 Recoloring을 사용하면 된다.
● Restructuring
Restructuring 수행 순서는 다음과 같다.
1. 나(z)와 내 부모(v), 내 부모의 부모(Grand Parent)를 오름차순으로 정렬
2. 무조건 가운데 있는 값을 부모로 만들고 나머지 둘을 자식으로 만든다.
3. 올라간 가운데 있는 값을 검정(Black)으로 만들고 그 두자식들을 빨강(Red)로 만든다.

Double Red가 발생한 트리에서 $w$가 검정색이기 때문에 Restructuring을 수행하는데, 1번을 수행하면 다음 그림과 같다.

여기서 2번을 수행하게 된다면, $z$가 부모 노드가 되고, 자식 노드로 $4$와 $7$이 들어오게 된다.

그리고 3번을 수행하여 색깔을 변경하면 다음 그림과 같아진다.

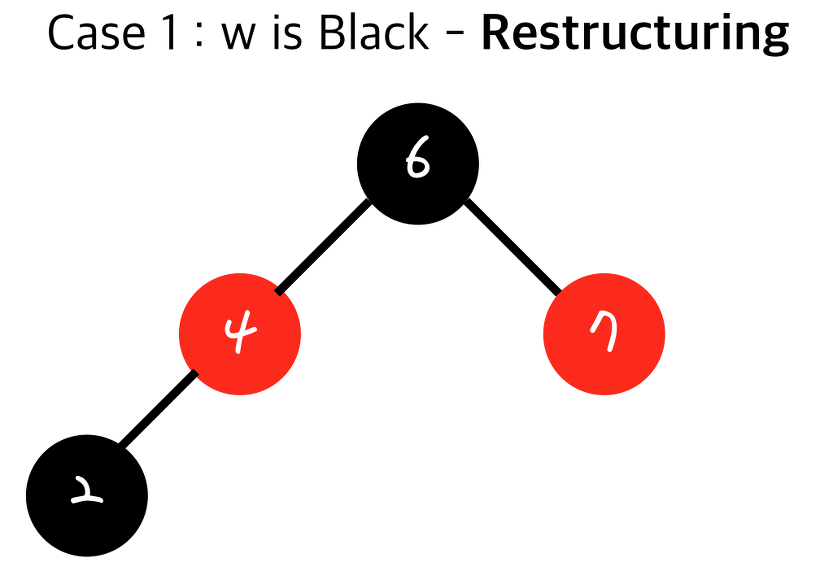
이로써 Restructuring을 수행하여 다시 규칙을 만족하는 레드-블랙 트리를 만들 수 있다.
참고 문헌에서는 쉽게 설명하기 위해 이런식으로 설명했지만 위키피디아에서는 설명이 다르게 되어 있다. 나와 부모 노드에 대해 RR 회전을 수행하고 나와 조상 노드에 대해 LL 회전을 수행한 후, 조상과
나의 컬러를 스위칭한다. 라고 설명할 수 있다. 자세한 내용은 위키피디아 삽입 부분을 참고한다.
이 방법은 다른 서브 트리에 영향을 끼치지 않고 자신과 부모와 조상 노드만 영향을 끼치므로 한번의 Restructuring만으로 규칙을 위배하지 않을 수 있다. Black Node의 수에 변화가 없기 때문에 4번 규칙 또한 위배되지 않는다. Restructuring 자체의 시간 복잡도는 $O(1)$이다.
(순서결정시간 - 상수시간, 트리로 만드는시간 - 상수시간, 원래있던 노드들의 구조들을 바꿔주는 시간 - 상수시간)
하지만 Restructuring은 어떤 노드가 삽입한 뒤에 수행되기 때문에 총 수행시간은 $O(logn)$이다.
● Recoloring
Recoloring의 수행 순서는 다음과 같다.
1. 현재 inset된 노드(z)의 부모(v)와 그 형제(w)를 검정(Black)으로 하고 Grand Parent(내 부모의 부모)를 빨강(Red)로 한다.
2. Grand Parent(내 부모의 부모)가 Root node가 아니었을 시 Double Red가 다시 발생 할 수 있다.

이번엔 uncle node가 빨간색인 경우이다.


1번을 수행하면 $w, v$ 의 색깔을 검정색으로, Grand Parent Node의 색깔을 빨간색으로 바꾼다.

하지만 레드-블랙 트리의 1번 조건으로 인해 root Node는 항상 검은색이므로 Grand Parent Node는 검정색으로 바꿔야한다. 이렇게 하면 Double Red를 해결할 수 있지만, 문제는 이 트리가 서브 트리라면, 이 트리에 상위 트리가 있고, Recoloring을 해도 또 Double Red가 발생할 수 있기 때문에 반복적으로 수행될 수 있다. 최악에 경우에는 root Node까지 반복될 수 있다. 만약 Double Red가 발생하면 다시 Restructuring 또는 Recoloring이 수행된다.
이것으로 노드를 삽입할 때 발생하는 방법들을 리뷰해봤는데, 사실 지금 기술한 내용들은 쉽게 기술된 내용이고 좀 더 자세한 내용이나 여러 케이스들에 대해서는 위키백과에 자세히 나와있기 때문에 이해가 됬다 생각하면 위키백과를 보도록 하자.
삭제
삭제는 삽입보다 좀 더 복잡하다. 삽입할 때는 조건을 만족하도록 넣으면 그만이지만, 삭제는 자칫하면 트리의 구조가 무너지기 때문이다. 예를 들어 검은색 노드를 삭제할 때, Black Height의 균형이 맞지 않게 되어 이를 해결하는 작업을 거쳐야 되기 때문이다.
아래 그림에서 $x$노드는 Black인 노드 $m$을 삭제하고 난 후의 자식 노드이다. 여기서 $x$인 노드는 non-leaf 자식이라는 개념을 갖는데, 트리에서 노드를 삭제할 때는 왼쪽 서브트리에서의 최댓값이나, 오른쪽 서브트리에서의 최솟값을 삭제한 노드의 위치에 삽입한다는 것이기 때문에 최대 한 개의 non-leaf 자식을 갖고 있는 노드를 삭제하는 문제로 치환할 수 있다라는 것이다.
삭제 또한 5개의 case와 재귀적으로 해결할 수 있다.

$p$의 왼쪽 자식 $m$이 삭제되고 Black Node인 $x$가 남았으므로 원래 Black 이였던 $m$이 삭제되면서 4번 조건인 Black Height가 맞지 않게 되었다.

이 경우에는 sibling Node의 색깔을 빨간색으로 바꾸고 부모 노드를 검정색으로 만들면 해결할 수 있다.

이번엔 전부 검정색인 경우이다.

$x$의 형제 노드인 $s$의 색깔을 빨간색으로 바꿔서 $x$의 부족한 Black Height를 $p$에다 전가한다. 이렇게 하면 $p$의 자식 노드의 Black Height는 균형을 맞추게 되고 하나의 서브 트리 $p$는 다시 재귀적으로 다른 케이스에서 해결하면 된다. 즉, 한번에 해결되진 않고 자식 노드의 Black Height만 해결하고 다시 큰 트리에서 Black Height를 맞추는 것이다.

형제 노드는 검정색, 형제 노드의 오른쪽 자식이 빨간색인 경우이다.
흰색 노드는 red 또는 black 일 경우이다. 즉, 두 가지 경우에도 만족한다는 뜻이다. 여기서 I가 빨간색이면 Black Height를 만족하는 것이 아니냐? 라고 생각할 수 있지만, 애초에 $p$ 자식 노드의 Black Height는 2라고 가정하고 $m$을 삭제했기 때문에 $l$이나 $r$ 자식 중에 검정색 노드가 있다는 뜻이다. 필자가 이것 때문이 많이 헷갈렸다.

Left Rotate을 한 뒤, $p$ 와 $s$의 색깔을 스위칭하고 $r$을 검은색으로 바꾸면 해결이 된다. 여기서도 $r$은 Black Height가 2인 가정이므로 검정색이 되기 때문에 Black Height는 변화가 없다.

이번엔 반대로 $l$이 빨간색이고 $r$이 검정색인 경우이다.

$s$를 기준으로 Right Rotate를 시켜주고 $l$과 $s$의 색깔을 스위칭한다. 그러면 case 3번과 똑같은 경우가 되기 때문에 (형제 노드는 검정색, 형제 노드의 오른쪽 자식이 빨간색인 경우) case 3번과 같은 처리를 해주면 된다.

대망의 마지막 케이스이다. $s$가 빨간색이고 $s$의 자식이 모두 검정색인 경우이다. (빨간색의 자식은 빨간색이 될 수 없음)

이 경우에는 $p$와 $s$의 색깔을 스위칭하고, $p$를 기준으로 Left Rotation을 진행한다. $x$의 Black Height는 해결되지 않았지만, $p$가 빨간색이고 $l$이 검정색이기 때문에 $l$의 자식 노드에 따라 위에 케이스 중 하나에 해당하게 된다. 다시 재귀 호출이 되는 것이다.
이렇게 레드-블랙 트리에서 노드를 삭제했을 때, Black Height를 해결할 수 있는 케이스들을 살펴보았다.
시간 복잡도
이러한 특성 때문에 레드-블랙 트리는 최고거나 최악인 경우에도 $O(logn)$의 복잡도를 보여준다.
검색, 삽입, 삭제시에 $O(logn)$의 시간 복잡도를 가진다. 균형잡힌 트리이고, 삽입과 삭제시 재귀적으로 트리의 균형이 맞춰지기 때문에 항상 $O(logn)$만큼 시간이 걸리는 것이다.
항상 짧고 비슷한 시간을 보장해주기 때문에 C++ STL에서 사용하고 게임 개발에 사용하는 이유라고 생각이 든다.
구현 및 테스트
https://github.com/XxMrEBAxX/Tree
GitHub - XxMrEBAxX/Tree
Contribute to XxMrEBAxX/Tree development by creating an account on GitHub.
github.com
이진 트리에서 가장 최악인 오름차순 데이터를 넣어보았다. 0~99까지 1을 더하면서 데이터를 삽입했는데, 이진 트리에서 이렇게 데이터 값을 넣으면 오른쪽 자식으로 길게 늘어진 순차 배열과 같은 트리의 구조를 보여주게 된다. 하지만 레드-블랙 트리에서는 어떻게 구조가 잡히는지 테스트하였다.

먼저 root Node는 31로 잡히게 되었다. 0~99 숫자 중 가운에데 위치한 숫자는 어림잡아 49 또는 50이여야 할테지만 레드-블랙 트리에서 트리의 균형을 어떻게든 맞춰본 숫자가 31인 것이다.
왼쪽 자식들을 보면 Black Height가 5인 것을 알 수 있다. (근 노드 색 제외) 정말로 레드-블랙 트리가 Black Height를 잘 맞춰놓았을지 오른쪽 자식들도 확인해보자.


왼쪽 자식에게선 없었던 빨간색 노드들이 눈에 띄기 시작한다. 분명히 잎 노드에서 출발해서 만나는 검정색 노드들의 수는 같다. 레드-블랙 트리는 데이터의 균형을 완벽히 맞추진 않았지만, 이진 트리에서의 최악의 데이터 삽입을 하였지만 어느정도 균형있는 구조를 유지하는 것을 확인할 수 있었다.

삭제 또한 정상적으로 진행이 되는 것을 확인했다. 트리 중간 지점에 있었던 87을 제거했더니 트리의 구조가 약간 바뀐 것을 확인할 수 있었다. 삭제된 노드의 값만 바뀐 것이 아니라 어느정도 여러개의 노드가 바뀐 것을 보면 재귀적으로 구조가 바뀌었다는 것을 알 수 있다. leaf node인 72를 삭제했더니 구조가 바뀌진 않고 72만 삭제된 모습도 확인할 수 있었다. Black Height 또한 잘 맞다.
'언어 > C++' 카테고리의 다른 글
| 암시적 변환(Implicit conversion) explicit (0) | 2025.05.30 |
|---|---|
| 템플릿 클래스 정의 선언 분리하기 (0) | 2025.05.26 |
| [c++] 멤버 변수의 초기화 순서 (0) | 2025.05.25 |


